DSA in Python (Day 1)

Problem Statement

QUESTION 1: Alice has some cards with numbers written on them. She arranges the cards in decreasing order, and lays them out face down in a sequence on a table. She challenges Bob to pick out the card containing a given number by turning over as few cards as possible. Write a function to help Bob locate the card.

Input

1. cards: A list of numbers sorted in decreasing order. E.g. [13, 11, 10, 7, 4, 3, 1, 0]
2. query: A number, whose position in the array is to be determined. E.g. 7

Output

1. position: The position of query in the list cards. E.g. 3 in the above case (counting from 0)

Solution:

Our function should be able to handle any set of valid inputs we pass into it. Here’s a list of some possible variations we might encounter:

1. The number query occurs somewhere in the middle of the list cards.
2. query is the first element in cards.
3. query is the last element in cards.
4. The list cards contains just one element, which is query.
5. The list cards does not contain number query.
6. The list cards is empty.
7. The list cards contains repeating numbers.
8. The number query occurs at more than one position in cards.

We will assume that our function will return -1 in case cards does not contain query.

In the case where query occurs multiple times in cards, we’ll expect our function to return the first occurrence of query.

Linear Search Algorithm:

def locate_card(cards, query):
    position = 0
    while position < len(cards):
        if cards[position] == query:
            return position
        position += 1
    return -1

The time complexity of linear search is O(N) and its space complexity is O(1).

Binary Search:

1. Binary search to find the index of any occurence of query:

def locate_card(cards, query):
    lo, hi = 0, len(cards) - 1

    while lo <= hi:
        mid = (lo + hi) // 2
        mid_number = cards[mid]

        if mid_number == query:
            return mid
        elif mid_number < query:
            hi = mid - 1
        elif mid_number > query:
            lo = mid + 1

    return -1

1. Binary search to find out first occurence of query:

def test_location(cards, query, mid):
    if cards[mid] == query:
        if mid-1 >= 0 and cards[mid-1] == query:
            return 'left'
        else:
            return 'found'
    elif cards[mid] < query:
        return 'left'
    else:
        return 'right'

def locate_card(cards, query):
    lo, hi = 0, len(cards) - 1
    while lo <= hi:
        mid = (lo + hi) // 2
        result = test_location(cards, query, mid)
        if result == 'found':
            return mid
        elif result == 'left':
            hi = mid - 1
        elif result == 'right':
            lo = mid + 1
    return -1

Complexity of Algorithm:

If we start out with an array of N elements, then each time the size of the array reduces to half for the next iteration, until we are left with just 1 element.

Initial length - N

Iteration 1 - N/2

Iteration 2 - N/4 i.e. N/2^2

Iteration 3 - N/8 i.e. N/2^3

…

Iteration k - N/2^k

Since the final length of the array is 1, we can find the

N/2^k = 1

Rearranging the terms, we get

N = 2^k

Taking the logarithm

k = log N

Where log refers to log to the base 2. Therefore, our algorithm has the time complexity O(log N). This fact is often stated as: binary search runs in logarithmic time. You can verify that the space complexity of binary search is O(1).

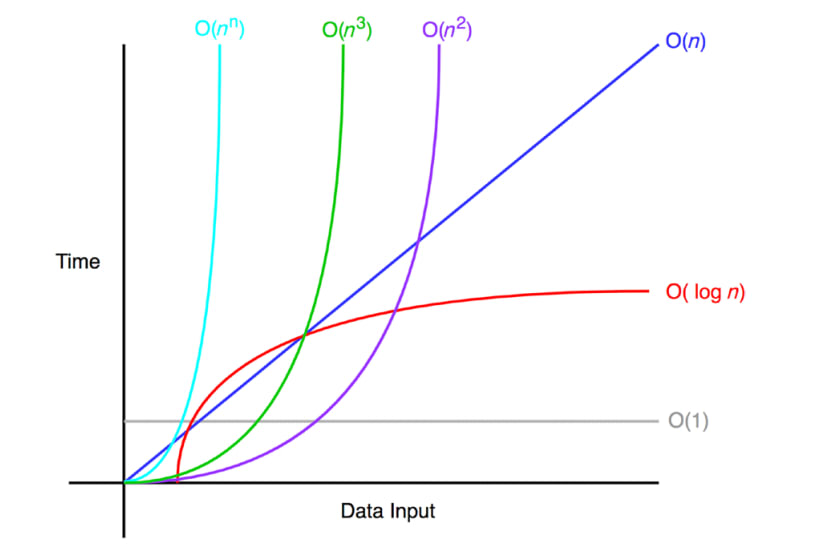
Binary search runs c * N / log N times faster than linear search, for some fixed constant c. Since log N grows very slowly compared to N, the difference gets larger with the size of the input. Here’s a graph showing how the comparing common functions for running time of algorithms:

Generic Binary Search:

def binary_search(lo, hi, condition):
    """TODO - add docs"""
    while lo <= hi:
        mid = (lo + hi) // 2
        result = condition(mid)
        if result == 'found':
            return mid
        elif result == 'left':
            hi = mid - 1
        else:
            lo = mid + 1
    return -1

We can now rewrite the locate_card function more succinctly using the binary_search function.

def locate_card(cards, query):

    def condition(mid):
        if cards[mid] == query:
            if mid > 0 and cards[mid-1] == query:
                return 'left'
            else:
                return 'found'
        elif cards[mid] < query:
            return 'left'
        else:
            return 'right'

    return binary_search(0,len(cards)-1,condition)

Question:

Given an array of integers nums sorted in ascending order, find the starting and ending position of a given number.

Answer:

def first_position(nums, target):
    def condition(mid):
        if nums[mid] == target:
            if mid > 0 and nums[mid-1] == target:
                return 'left'
            return 'found'
        elif nums[mid] < target:
            return 'right'
        else:
            return 'left'
    return binary_search(0, len(nums)-1, condition)

def last_position(nums, target):
    def condition(mid):
        if nums[mid] == target:
            if mid < len(nums)-1 and nums[mid+1] == target:
                return 'right'
            return 'found'
        elif nums[mid] < target:
            return 'right'
        else:
            return 'left'
    return binary_search(0, len(nums)-1, condition)

def first_and_last_position(nums, target):
    return first_position(nums, target), last_position(nums, target)

Problems for Practice

Here are some resources to learn more and find problems to practice.

• Binary Search Problems on LeetCode: Link
• Binary Search Problems on GeeksForGeeks: Link
• Binary Search Problems on Codeforces: Link