Problem Statement
QUESTION 1: As a senior backend engineer at Jovian, you are tasked with developing a fast in-memory data structure to manage profile information (username, name and email) for 100 million users. It should allow the following operations to be performed efficiently:
- Insert the profile information for a new user.
- Find the profile information of a user, given their username
- Update the profile information of a user, given their usrname
- List all the users of the platform, sorted by username
You can assume that usernames are unique.
Problem
We need to create a data structure which can store 100 million records and perform insertion, search, update and list operations efficiently.
Input
The key inputs to our data structure are user profiles, which contain the username, name and email of a user.
1
2
3
4
5
6
7
8
9
10
11
class User:
def __init__(self, username, name, email):
self.username = username
self.name = name
self.email = email
def __repr__(self):
return "User(username='{}', name='{}', email='{}')".format(self.username, self.name, self.email)
def __str__(self):
return self.__repr__()
let’s create some users,
1
2
3
4
5
6
7
aakash = User('aakash', 'Aakash Rai', 'aakash@example.com')
biraj = User('biraj', 'Biraj Das', 'biraj@example.com')
hemanth = User('hemanth', 'Hemanth Jain', 'hemanth@example.com')
jadhesh = User('jadhesh', 'Jadhesh Verma', 'jadhesh@example.com')
siddhant = User('siddhant', 'Siddhant Sinha', 'siddhant@example.com')
sonaksh = User('sonaksh', 'Sonaksh Kumar', 'sonaksh@example.com')
vishal = User('vishal', 'Vishal Goel', 'vishal@example.com')
1
users = [aakash, biraj, hemanth, jadhesh, siddhant, sonaksh, vishal]
Output
We can also express our desired data structure as a Python class UserDatabase with four methods: insert, find, update and list_all.
1
2
3
4
5
6
7
8
9
10
11
12
class UserDatabase:
def insert(self, user):
pass
def find(self, username):
pass
def update(self, user):
pass
def list_all(self):
pass
Here’s a simple and easy solution to the problem: we store the User objects in a list sorted by usernames.
The various functions can be implemented as follows:
- Insert: Loop through the list and add the new user at a position that keeps the list sorted.
- Find: Loop through the list and find the user object with the username matching the query.
- Update: Loop through the list, find the user object matching the query and update the details
- List: Return the list of user objects.
We can use the fact usernames, which are are strings can be compared using the <, > and == operators in Python.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class UserDatabase:
def __init__(self):
self.users = []
def insert(self, user):
i = 0
while i < len(self.users):
# Find the first username greater than the new user's username
if self.users[i].username > user.username:
break
i += 1
self.users.insert(i, user)
def find(self, username):
for user in self.users:
if user.username == username:
return user
def update(self, user):
target = self.find(user.username)
target.name, target.email = user.name, user.email
def list_all(self):
return self.users
We can create a new database of users by instantiating and object of the UserDatabase class.
1
database = UserDatabase()
Analyze the algorithm’s complexity and identify inefficiencies
The operations insert, find, update involves iterating over a list of users, in the worst case, they may take up to N iterations to return a result, where N is the total number of users. list_all however, simply returns the existing internal list of users.
Thus, the time complexities of the various operations are:
- Insert: O(N)
- Find: O(N)
- Update: O(N)
- List: O(1)
Balanced Binary Search Trees
For our use case, we require the binary tree to have some additional properties:
- Keys and Values: Each node of the tree stores a key (a username) and a value (a
Userobject). Only keys are shown in the picture above for brevity. A binary tree where nodes have both a key and a value is often referred to as a map or treemap (because it maps keys to values). - Binary Search Tree: The left subtree of any node only contains nodes with keys that are lexicographically smaller than the node’s key, and the right subtree of any node only contains nodes with keys that lexicographically larger than the node’s key. A tree that satisfies this property is called a binary search trees, and it’s easy to locate a specific key by traversing a single path down from the root note.
- Balanced Tree: The tree is balanced i.e. it does not skew too heavily to one side or the other. The left and right subtrees of any node shouldn’t differ in height/depth by more than 1 level.
Height of a Binary Tree
The number of levels in a tree is called its height. As you can tell from the picture above, each level of a tree contains twice as many nodes as the previous level.
For a tree of height k, here’s a list of the number of nodes at each level:
Level 0: 1
Level 1: 2
Level 2: 4 i.e. 2^2
Level 3: 8 i.e. 2^3
…
Level k-1: 2^(k-1)
If the total number of nodes in the tree is N, then it follows that
1
N = 1 + 2^1 + 2^2 + 2^3 + ... + 2^(k-1)
We can simplify this equation by adding 1 on each side:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
N + 1 = 1 + 1 + 2^1 + 2^2 + 2^3 + ... + 2^(k-1)
N + 1 = 2^1 + 2^1 + 2^2+ 2^3 + ... + 2^(k-1)
N + 1 = = 2^2 + 2^2 + 2^3 + ... + 2^(k-1)
N + 1 = = 2^3 + 2^3 + ... + 2^(k-1)
...
N + 1 = 2^(k-1) + 2^(k-1)
N + 1 = 2^k
k = log(N + 1) <= log(N) + 1
Thus, to store N records we require a balanced binary search tree (BST) of height no larger than log(N) + 1. This is a very useful property, in combination with the fact that nodes are arranged in a way that makes it easy to find a specific key by following a single path down from the root.
As we’ll see soon, the insert, find and update operations in a balanced BST have time complexity O(log N) since they all involve traversing a single path down from the root of the tree.
Binary Tree
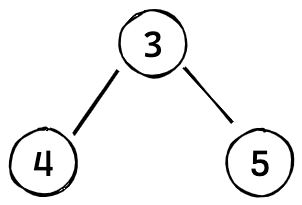
QUESTION 2: Implement a binary tree using Python, and show its usage with some examples.
To begin, we’ll create simple binary tree (without any of the additional properties) containing numbers as keys within nodes. Here’s an example:
Here’s a simple class representing a node within a binary tree.
1
2
3
4
5
class TreeNode:
def __init__(self, key):
self.key = key
self.left = None
self.right = None
Let’s create objects representing each node of the above tree
1
2
3
node0 = TreeNode(3)
node1 = TreeNode(4)
node2 = TreeNode(5)
We can connect the nodes by setting the .left and .right properties of the root node.
1
2
node0.left = node1
node0.right = node2
And we’re done! We can create a new variable tree which simply points to the root node, and use it to access all the nodes within the tree.
1
tree = node0
Going forward, we’ll use the term “tree” to refer to the root node. The term “node” can refer to any node in a tree, not necessarily the root.
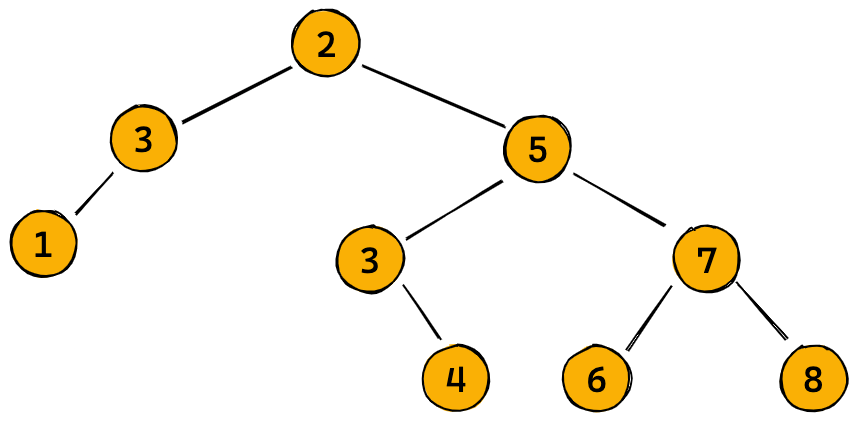
Exercise: Create the following binary tree using the TreeNode class defined above.
It’s a bit inconvenient to create a tree by manually connecting all the nodes. Let’s write a helper function which can convert a tuple with the structure ( left_subtree, key, right_subtree) (where left_subtree and right_subtree are themselves tuples) into binary tree.
Here’s an tuple representing the tree shown above:
1
tree_tuple = ((1,3,None), 2, ((None, 3, 4), 5, (6, 7, 8)))
1
2
3
4
5
6
7
8
9
10
11
def parse_tuple(data):
# print(data)
if isinstance(data, tuple) and len(data) == 3:
node = TreeNode(data[1])
node.left = parse_tuple(data[0])
node.right = parse_tuple(data[2])
elif data is None:
node = None
else:
node = TreeNode(data)
return node
1
tree = parse_tuple(tree_tuple)
Exercise: Define a function tree_to_tuple that converts a binary tree into a tuple representing the same tree. E.g. tree_to_tuple converts the tree created above to the tuple ((1, 3, None), 2, ((None, 3, 4), 5, (6, 7, 8))). Hint: Use recursion.
1
2
3
4
5
6
def tree_to_tuple(node):
if node is None:
return None
if node.left is None and node.right is None:
return node.key
return tree_to_tuple(node.left), node.key, tree_to_tuple(node.right)
Let’s create another helper function to display all the keys in a tree-like structure for easier visualization.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
def display_keys(node, space='\t', level=0):
# print(node.key if node else None, level)
# If the node is empty
if node is None:
print(space*level + '∅')
return
# If the node is a leaf
if node.left is None and node.right is None:
print(space*level + str(node.key))
return
# If the node has children
display_keys(node.right, space, level+1)
print(space*level + str(node.key))
display_keys(node.left,space, level+1)
Let’s try using the function.
1
display_keys(tree, ' ')
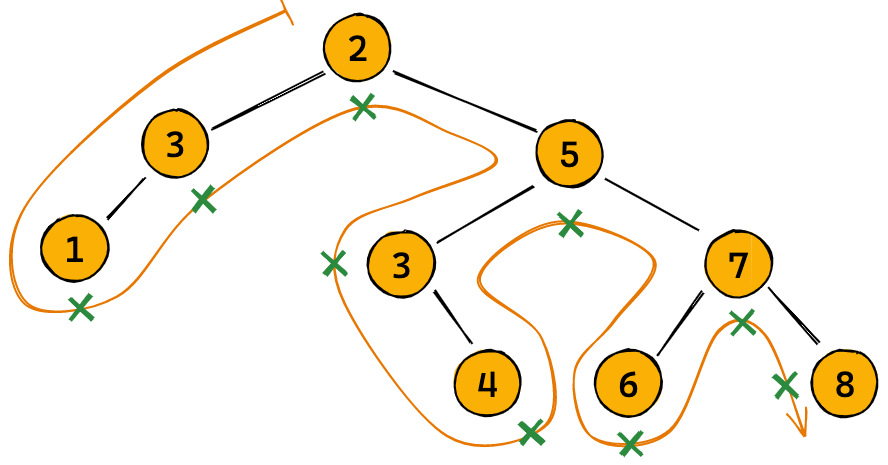
Traversing a Binary Tree
The following questions are frequently asked in coding interviews and assessments:
QUESTION: Write a function to perform the inorder traversal of a binary tree.
QUESTION: Write a function to perform the preorder traversal of a binary tree.
QUESTION: Write a function to perform the postorder traversal of a binary tree.
A traversal refers to the process of visiting each node of a tree exactly once. Visiting a node generally refers to adding the node’s key to a list. There are three ways to traverse a binary tree and return the list of visited keys:
Inorder traversal
- Traverse the left subtree recursively inorder.
- Traverse the current node.
- Traverse the right subtree recursively inorder.
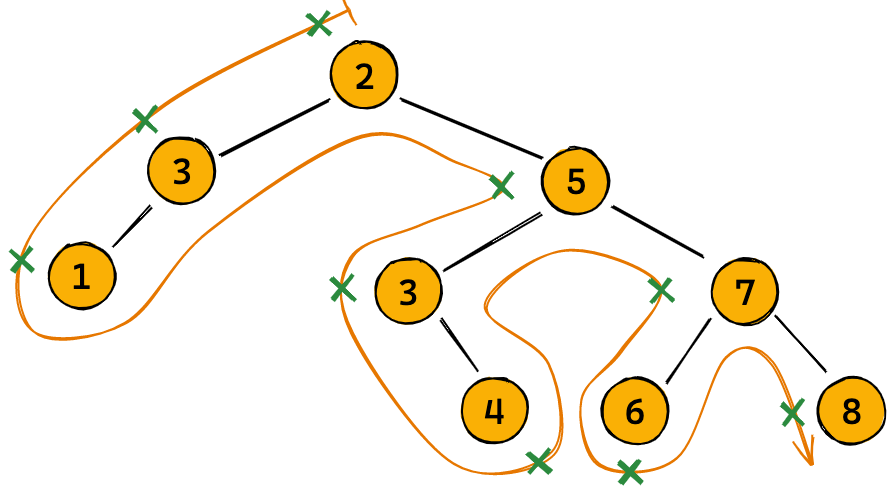
Preorder traversal
- Traverse the current node.
- Traverse the left subtree recursively preorder.
- Traverse the right subtree recursively preorder.
Can you guess how postorder traversal works??
Here’s an implementation of inorder traversal of a binary tree.
1
2
3
4
5
6
def traverse_in_order(node):
if node is None:
return []
return(traverse_in_order(node.left) +
[node.key] +
traverse_in_order(node.right))
Height and Size of a Binary Tree
QUESTION: Write a function to calculate the height/depth of a binary tree
QUESTION: Write a function to count the number of nodes in a binary tree
The height/depth of a binary tree is defined as the length of the longest path from its root node to a leaf. It can be computed recursively, as follows:
1
2
3
4
def tree_height(node):
if node is None:
return 0
return 1 + max(tree_height(node.left), tree_height(node.right))
Here’s a function to count the number of nodes in a binary tree.
1
2
3
4
def tree_size(node):
if node is None:
return 0
return 1 + tree_size(node.left) + tree_size(node.right)
As a final step, let’s compile all the functions we’ve written so far as methods withing the TreeNode class itself. Encapsulation of data and functionality within the same class is a good programming practice.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
class TreeNode():
def __init__(self, key):
self.key, self.left, self.right = key, None, None
def height(self):
if self is None:
return 0
return 1 + max(TreeNode.height(self.left), TreeNode.height(self.right))
def min_height(self):
if self in None:
return 0
elif self.left is None:
return 1 + TreeNode.min_height(self.right)
elif self.right is None:
return 1 + TreeNode.min_height(self.left)
return 1 + min(TreeNode.min_height(self.left), TreeNode.min_height(self.right))
def size(self):
if self is None:
return 0
return 1 + TreeNode.size(self.left) + TreeNode.size(self.right)
def diameter():
self.diameter = 0
def get_max_depth(node):
if node is None:
return 0
left_max_depth = get_max_depth(node.left)
right_max_depth = get_max_depth(node.right)
self.diameter = max(self.diameter, left_max_depth+right_max_depth)
return 1 + max(left_max_depth,right_max_depth)
get_max_depth(self)
return self.diameter
def traverse_in_order(self):
if self is None:
return []
return (TreeNode.traverse_in_order(self.left) +
[self.key] +
TreeNode.traverse_in_order(self.right))
def traverse_preorder(self):
if self in None:
return []
return ([self.key]+TreeNode.traverse_preorder(self.left)+
TreeNode.traverse_preorder(self.right))
def traverse_postorder(self):
if self is None:
return []
return (Treenode.traverse_postorder(self.left)+
TreeNode.traverse_postorder(self.right)+[self.key])
def display_keys(self, space='\t', level=0):
# If the node is empty
if self is None:
print(space*level + '∅')
return
# If the node is a leaf
if self.left is None and self.right is None:
print(space*level + str(self.key))
return
# If the node has children
display_keys(self.right, space, level+1)
print(space*level + str(self.key))
display_keys(self.left,space, level+1)
def to_tuple(self):
if self is None:
return None
if self.left is None and self.right is None:
return self.key
return TreeNode.to_tuple(self.left), self.key, TreeNode.to_tuple(self.right)
def __str__(self):
return "BinaryTree <{}>".format(self.to_tuple())
def __repr__(self):
return "BinaryTree <{}>".format(self.to_tuple())
@staticmethod
def parse_tuple(data):
if data is None:
node = None
elif isinstance(data, tuple) and len(data) == 3:
node = TreeNode(data[1])
node.left = TreeNode.parse_tuple(data[0])
node.right = TreeNode.parse_tuple(data[2])
else:
node = TreeNode(data)
return node
Binary Search Tree (BST)
A binary search tree or BST is a binary tree that satisfies the following conditions:
- The left subtree of any node only contains nodes with keys less than the node’s key
- The right subtree of any node only contains nodes with keys greater than the node’s key
It follows from the above conditions that every subtree of a binary search tree must also be a binary search tree.
QUESTION: Write a function to check if a binary tree is a binary search tree (BST).
QUESTION: Write a function to find the maximum key in a binary tree.
QUESTION: Write a function to find the minimum key in a binary tree.
Here’s a function that covers all of the above:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
def remove_none(nums):
return [x for x in nums if x is not None]
def is_bst(node):
if node is None:
return True, None, None
is_bst_l, min_l, max_l = is_bst(node.left)
is_bst_r, min_r, max_r = is_bst(node.right)
is_bst_node = (is_bst_l and is_bst_r and
(max_l is None or node.key > max_l) and
(min_r is None or node.key < min_r))
min_key = min(remove_none([min_l, node.key, min_r]))
max_key = max(remove_none([max_l, node.key, max_r]))
# print(node.key, min_key, max_key, is_bst_node)
return is_bst_node, min_key, max_key
Storing Key-Value Pairs using BSTs
Recall that we need to store user objects with each key in our BST. Let’s define new class BSTNode to represent the nodes of of our tree. Apart from having properties key, left and right, we’ll also store a value and pointer to the parent node (for easier upward traversal).
1
2
3
4
5
6
7
class BSTNode():
def __init__(self, key, value=None):
self.key = key
self.value = value
self.left = None
self.right = None
self.parent = None
Let’s try to recreate this BST with usernames as keys and user objects as values: 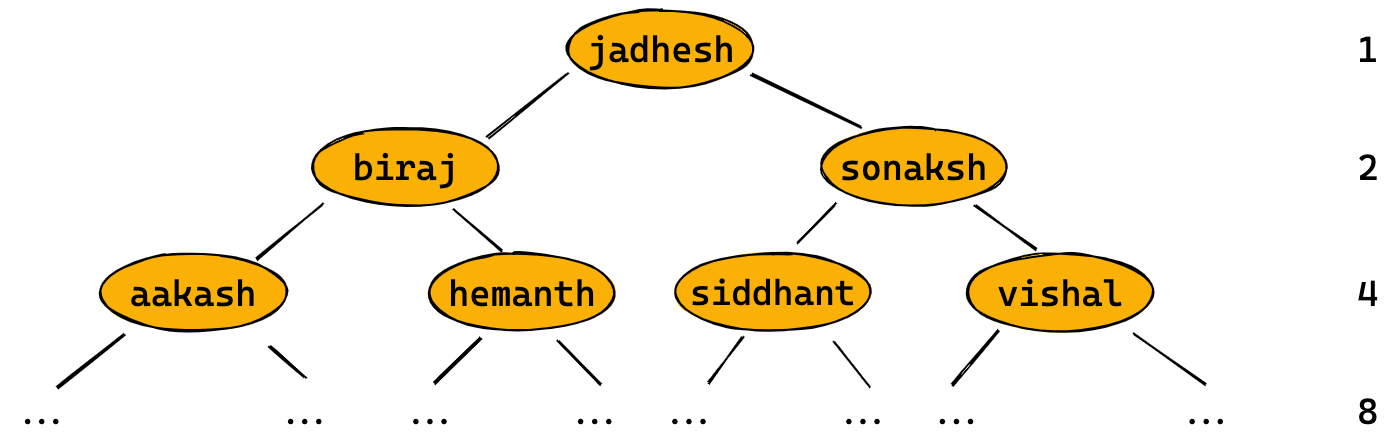
1
2
3
4
5
6
7
tree = BSTNode(jadhesh.username, jadhesh)
tree.left = BSTNode(biraj.username, biraj)
tree.right = BSTNode(sonaksh.username, sonaksh)
.
..
...
#here jadhesh,biraj,sonaksh are the instance of User class created earlier
Insertion into BST
QUESTION: Write a function to insert a new node into a BST.
We use the BST-property to perform insertion efficiently:
- Starting from the root node, we compare the key to be inserted with the current node’s key
- If the key is smaller, we recursively insert it in the left subtree (if it exists) or attach it as as the left child if no left subtree exists.
- If the key is larger, we recursively insert it in the right subtree (if it exists) or attach it as as the right child if no right subtree exists.
Here’s a recursive implementation of insert.
1
2
3
4
5
6
7
8
9
10
def insert(node, key, value):
if node is None:
node = BSTNode(key, value)
elif key < node.key:
node.left = insert(node.left, key, value)
node.left.parent = node
elif key > node.key:
node.right = insert(node.right, key, value)
node.right.parent = node
return node
1
2
3
4
5
6
7
tree = insert(None, jadhesh.username, jadhesh)
insert(tree, biraj.username, biraj)
insert(tree, sonaksh.username, sonaksh)
insert(tree, aakash.username, aakash)
insert(tree, hemanth.username, hemanth)
insert(tree, siddhant.username, siddhant)
insert(tree, vishal.username, siddhant)
Note, however, that the order of insertion of nodes change the structure of the resulting tree.
1
2
3
4
5
6
7
tree2 = insert(None, aakash.username, aakash)
insert(tree2, biraj.username, biraj)
insert(tree2, hemanth.username, hemanth)
insert(tree2, jadhesh.username, jadhesh)
insert(tree2, siddhant.username, siddhant)
insert(tree2, sonaksh.username, sonaksh)
insert(tree2, vishal.username, vishal)
Skewed/unbalanced BSTs are problematic because the height of such trees often ceases to logarithmic compared to the number of nodes in the tree. For instance the above tree has 7 nodes and height 7.
The length of the path traversed by insert is equal to the height of the tree (in the worst case). It follows that if the tree is balanced, the time complexity of insertion is O(log N) otherwise it is O(N).
Finding a Node in BST
QUESTION: Find the value associated with a given key in a BST.
We can follow a recursive strategy similar to insertion to find the node with a given key within a BST.
1
2
3
4
5
6
7
8
9
def find(node, key):
if node is None:
return None
if key == node.key:
return node
if key < node.key:
return find(node.left, key)
if key > node.key:
return find(node.right, key)
Updating a value in a BST
QUESTION: Write a function to update the value associated with a given key within a BST
We can use find to locate the node to be updated, and simply update it’s value.
1
2
3
4
def update(node, key, value):
target = find(node, key)
if target is not None:
target.value = value
List the nodes
QUESTION: Write a function to retrieve all the key-values pairs stored in a BST in the sorted order of keys.
The nodes can be listed in sorted order by performing an inorder traversal of the BST.
1
2
3
4
def list_all(node):
if node is None:
return []
return list_all(node.left) + [(node.key, node.value)] + list_all(node.right)
Balanced Binary Trees
QUESTION: Write a function to determine if a binary tree is balanced.
Here’s a recursive strategy:
- Ensure that the left subtree is balanced.
- Ensure that the right subtree is balanced.
- Ensure that the difference between heights of left subtree and right subtree is not more than 1.
1
2
3
4
5
6
7
8
def is_balanced(node):
if node is None:
return True, 0
balanced_l, height_l = is_balanced(node.left)
balanced_r, height_r = is_balanced(node.right)
balanced = balanced_l and balanced_r and abs(height_l - height_r) <=1
height = 1 + max(height_l, height_r)
return balanced, height
Balanced Binary Search Trees
QUESTION: Write a function to create a balanced BST from a sorted list/array of key-value pairs.
We can use a recursive strategy here, turning the middle element of the list into the root, and recursively creating left and right subtrees.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
def make_balanced_bst(data, lo=0, hi=None, parent=None):
if hi is None:
hi = len(data) - 1
if lo > hi:
return None
mid = (lo + hi) // 2
key, value = data[mid]
root = BSTNode(key, value)
root.parent = parent
root.left = make_balanced_bst(data, lo, mid-1, root)
root.right = make_balanced_bst(data, mid+1, hi, root)
return root
Balancing an Unbalanced BST
QUESTION: Write a function to balance an unbalanced binary search tree.
We first perform an inorder traversal, then create a balanced BST using the function defined earlier.
1
2
def balance_bst(node):
return make_balanced_bst(list_all(node))
Complexity of the various operations in a balanced BST:
- Insert - O(log N) + O(N) = O(N)
- Find - O(log N)
- Update - O(log N)
- List all - O(N)
A Python-Friendly Treemap
We are now ready to return to our original problem statement. We can create a generic class TreeMap which supports all the operations specified in the original problem statement in a python-friendly manner.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class TreeMap():
def __init__(self):
self.root = None
def __setitem__(self, key, value):
node = find(self.root, key)
if not node:
self.root = insert(self.root, key, value)
self.root = balance_bst(self.root)
else:
update(self.root, key, value)
def __getitem__(self, key):
node = find(self.root, key)
return node.value if node else None
def __iter__(self):
return (x for x in list_all(self.root))
def __len__(self):
return tree_size(self.root)
def display(self):
return display_keys(self.root)